推荐系统项目实战一(推荐业务架构介绍)
本文共 358 字,大约阅读时间需要 1 分钟。
架构与业务流
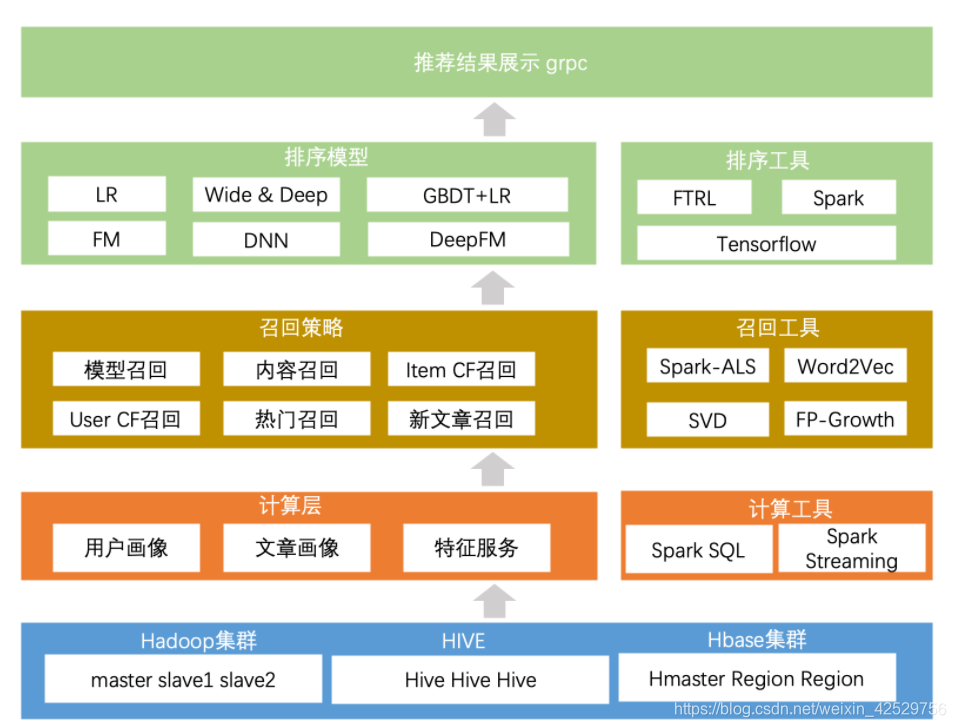
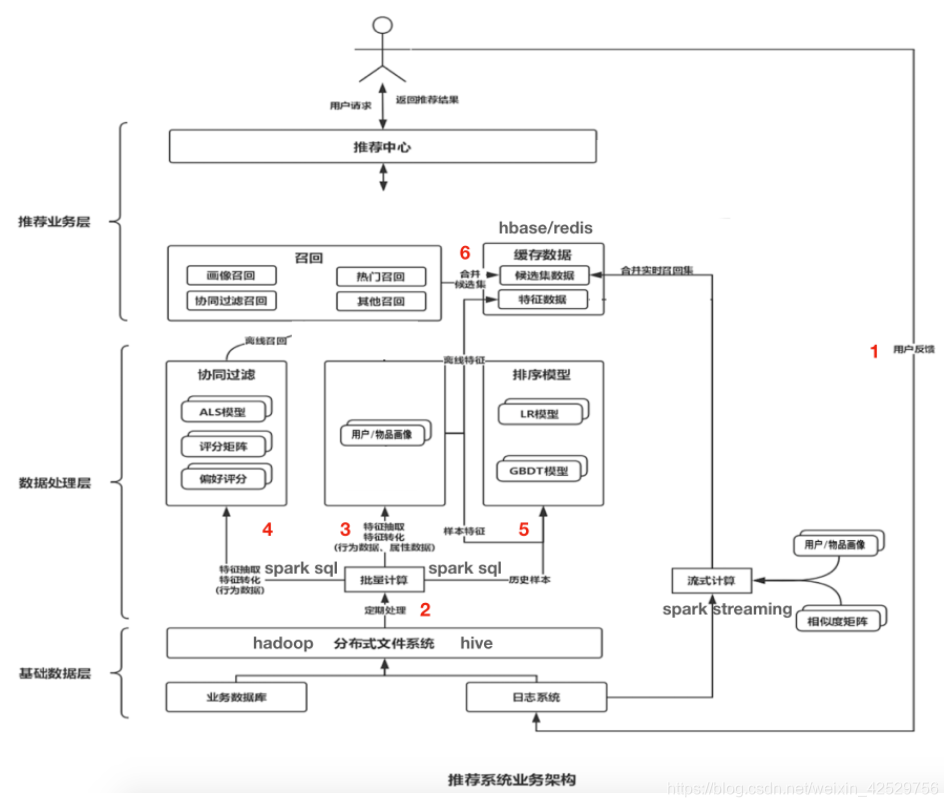
- 基础数据层:
- 包括业务数据和用户行为日志数据。
- 业务数据主要包含用户数据和文章数据,用户数据即某头条注册用户的基础数据,文章数据在自媒体平台上传的文章的基本信息。
- 用户行为日志数据来源于前端埋点
- 业务批量存储在HDFS上以用作离线分析
- 日志数据实时流向Kafka以用作实时计算
- 包括业务数据和用户行为日志数据。
- 数据处理层:
- 基础计算:基于离线和实时数据,对各类基础数据计算成用户画像、文章画像
- 召回与排序
- 召回环节使用各种算法逻辑从海量的文章中筛选出用户感兴趣的文章候选集合,集合大小:上千级别。排序即对候选集合中的文章进行用户相对的模型结果排序,生成一个排序列表。
- 召回
- 排序
- 点击率预估模型
- 特征处理、模型评价
- 推荐业务层:通过对外提供rpc接口来实现推荐业务的接入
- Feed流推荐:今日推荐场景,用户可以在这些页面中不断下拉刷新
转载地址:http://jvxp.baihongyu.com/
你可能感兴趣的文章